生成式算法概述
现有的生成式算法可以大体分为基于似然的方法(likelihood-based methods)、基于自回归的方法(autoregressive-based methods) 以及基于GAN的方法。本页笔记对这三种方法进行简要的概述。
1 基于似然的方法
顾名思义,基于似然的方法通过最大化似然函数的方式来对模型参数进行优化。著名的基于似然的算法包括变分自编码器(Variational autoencoders, VAE),基于流的模型(flow-based models),以及目前大火的diffusion算法。之后简单介绍VAE和flow-based model 的思想,关于difffusion将在之后单独开一页笔记记录。
1.1 Variational autoencoders
VAE的具体结构如下图所示。输入经过编码器后,得到分布的均值和方差。利用重参数化技巧,根据得到的均值和方差,获得隐变量的正态分布。从正态分布中采样后,解码获得输出。通过这种方式,以输入嵌入为中心,其周围的数据输出将属于同一种类型。VAE的损失函数由两项组成,一项是最小化重建损失,同自编码器;另一部分是最小化下图中右下角黄色框中的多项式。
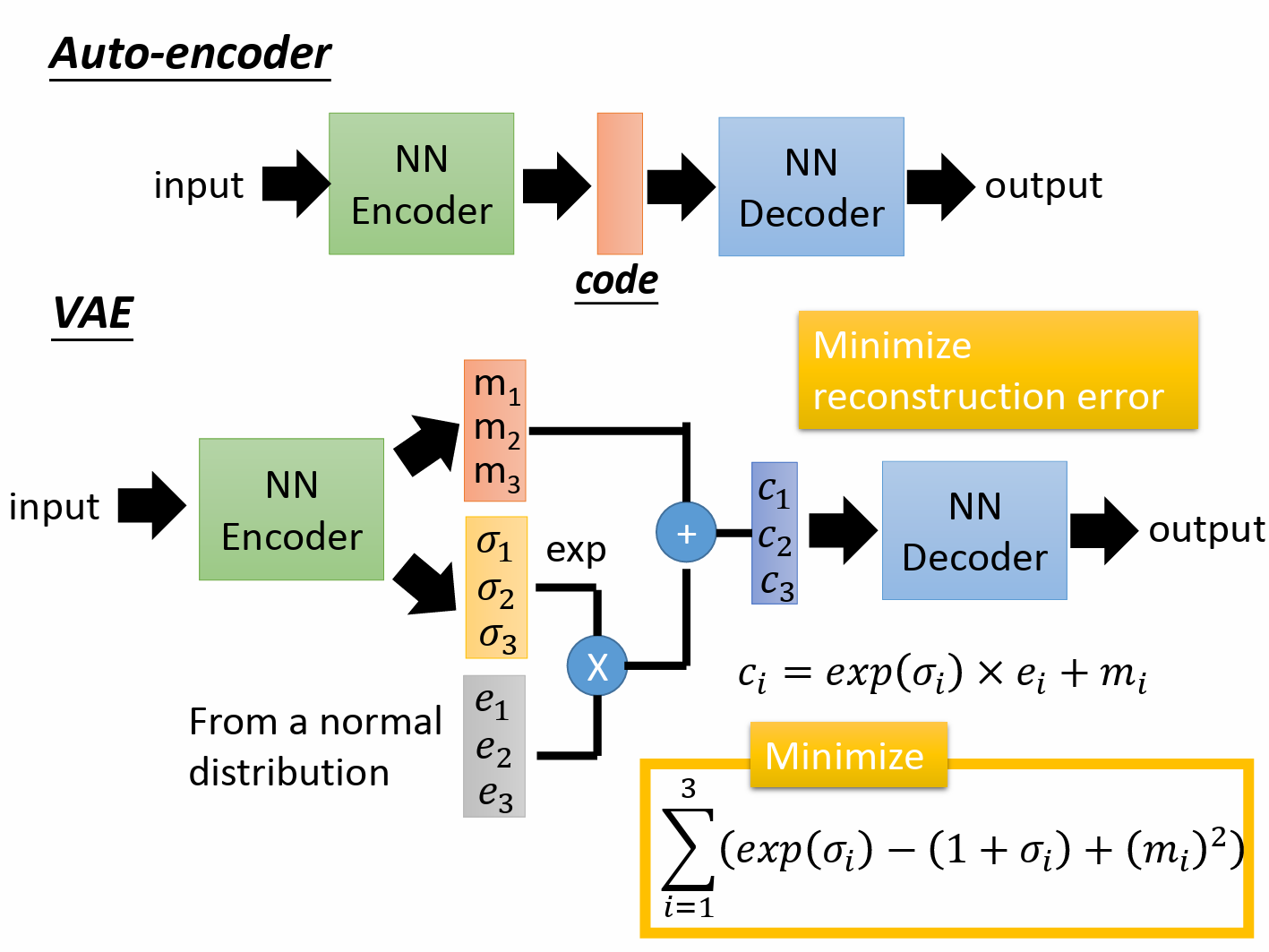
从直观的角度来看,黄色框中的项起到了正则的作用,约束隐变量的均值尽可能接近于0,方差接近于1(若是不对方差进行约束,方差趋近为0,则VAE退化为AE,丧失了其作用)。约束均值尽可能接近0,使得不同类别的分布尽可能靠近,从而压缩隐空间的分布范围,使隐空间分布相对于输入空间更加密集。
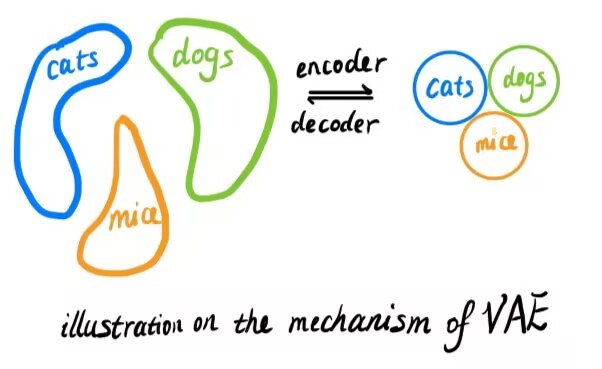
而从数学的角度来看,VAE是在优化似然函数 $logP(x)$ 的变分下界。详细的推导可参见 该pdf 。
1.2 flow-based models
基于流的方法希望获得一个生成器,使得输入满足高斯分布,而输出分布与目标数据分布尽可能一致(即两者KL散度小)。可以证明,最小化KL散度和极大似然等效,因而优化目标是极大似然问题。
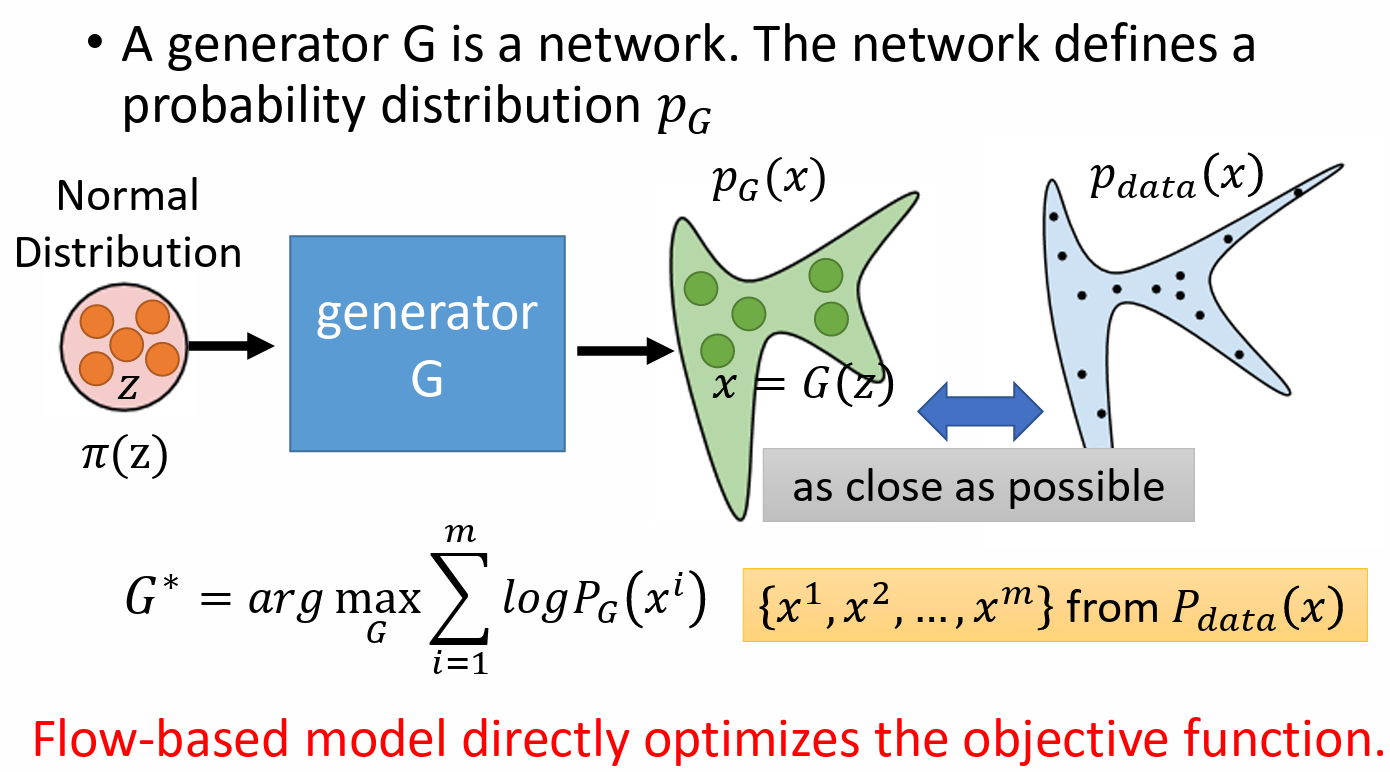
由概率与统计的知识可知,随机变量 Z 和 X 之间满足如下关系:
\[\pi(z) =\left| J_{G} \right| p_{G}(x)\]其中 $ J_{G}$ 为函数G的雅可比矩阵。该式可变形为
\[p_{G}(x)=\left| J_{G^{-1}} \right|\pi(G^{-1}(x))\]可以看到,对上式进行优化需要解决两件事:
- 如何求 $J_{G^{-1}}$ ;
- 如何求 $G^{-1}(x)$ ;
目前常见的两种策略是使用Coupling Layer和1x1 Convolution(参考该pdf)。
此外,由于一层生成器的空间转化能力可能不足,所以往往采用多层生成器级联的方式。

VAE 和 flow-based 方法速度较快,相比GAN比较容易优化,但和GAN相比,合成的图片质量较差。
2 基于自回归的方法
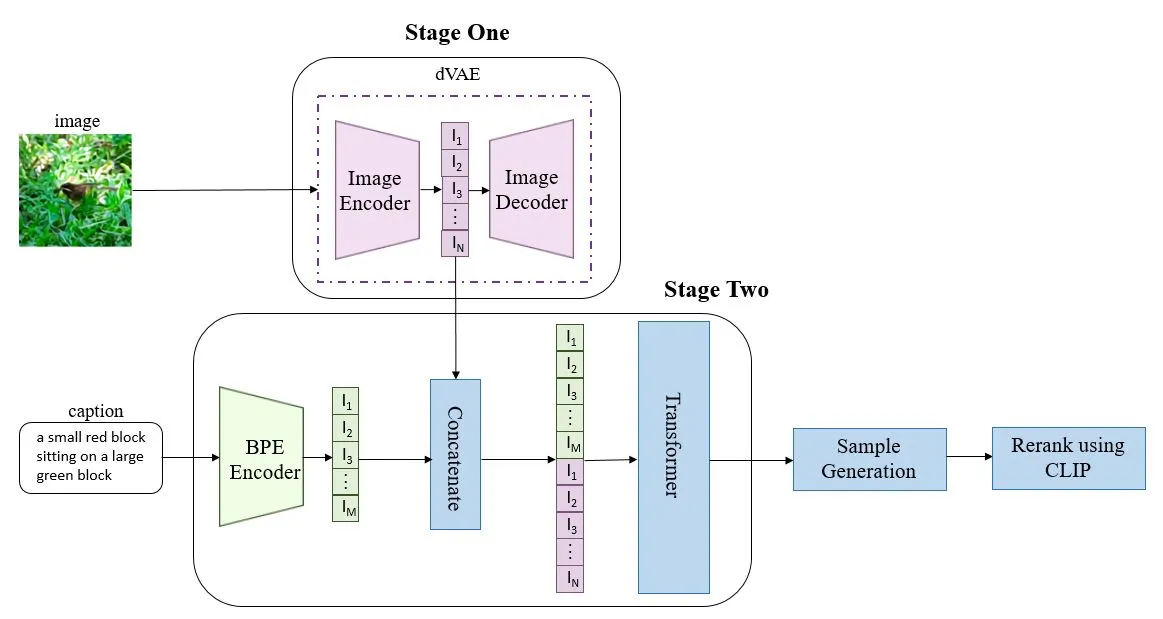
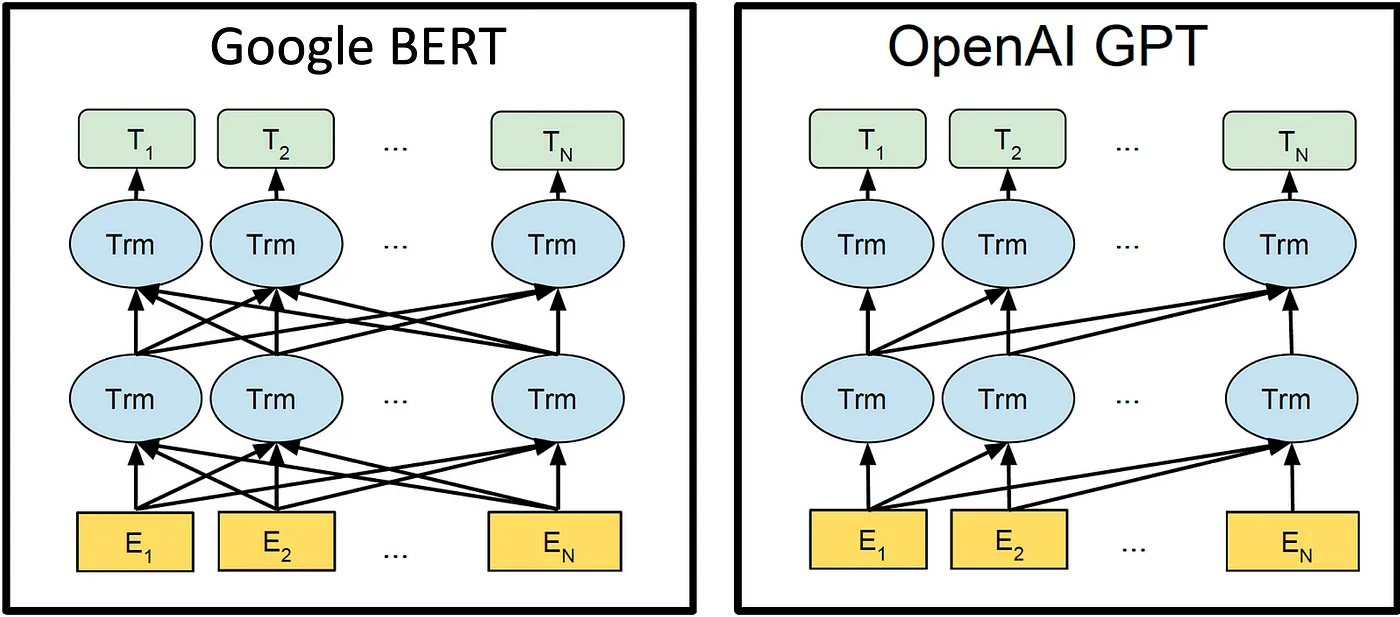
经典的基于自回归的方法包括PixelRNN和PixelCNN。当前在NLP方面,大火的GPT系列模型 (见下方图2) 基于自回归方法工作; 而DALL-E(见下方图1) 等自回归方法在CV领域也取得了广泛的成功。
自回归方法简单的说,就是根据现有预测结果,预测序列下一个token的结果,将得到token的结果包含进预测结果序列中,继续重复进行预测,直到检测到结束标识为止。
相比其他方法, 基于自回归的方法合成质量较高,缺点在于合成速度很慢。
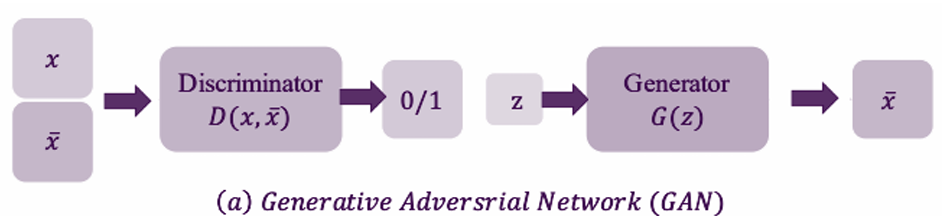
3 基于GAN的方法
基于GAN的方法曾经引领了CV中图像生成的潮流, 其利用生成器将正态分布转化为目标分布,利用判别器判断图片是否为合成图。
GAN以其高合成质量而闻名,但缺点在于,优化困难(即很难训)。