Transducer 系列模型
语音识别的一大难点在于其 输入(音频) 和 输出(文本) 之间并不是等长的。如何处理输入和输出之间对齐关系是 ASR 中的核心问题之一。
1 CTC
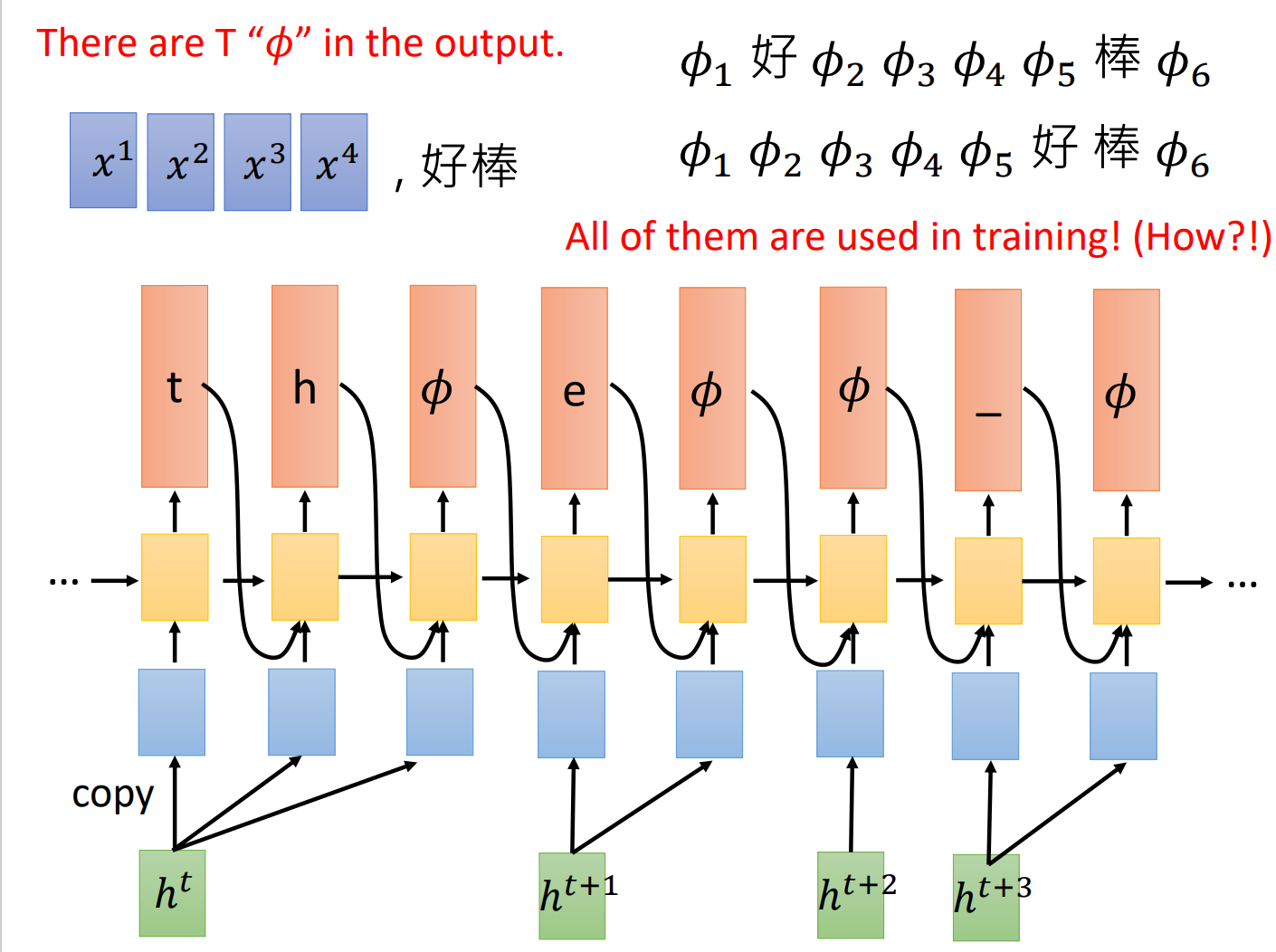
CTC 是早期的 语音识别方案,其结构如下所示。在CTC结构中,输入和输出是等长的。其对齐方式可以通过以下图片说明:
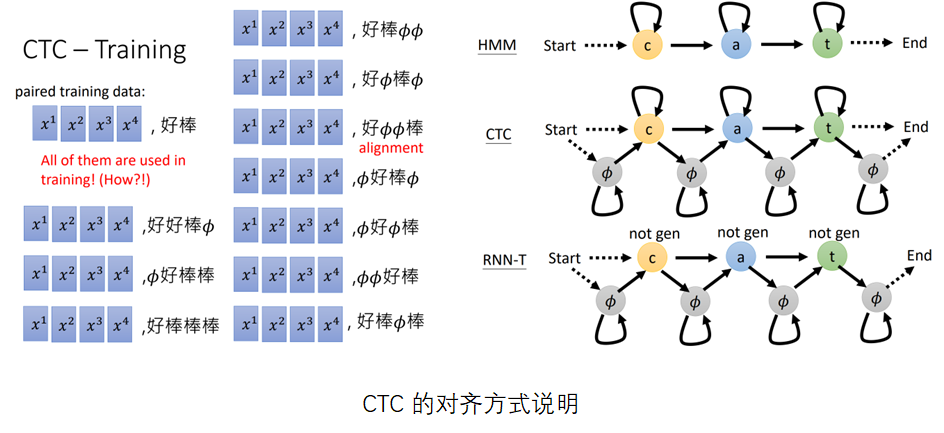
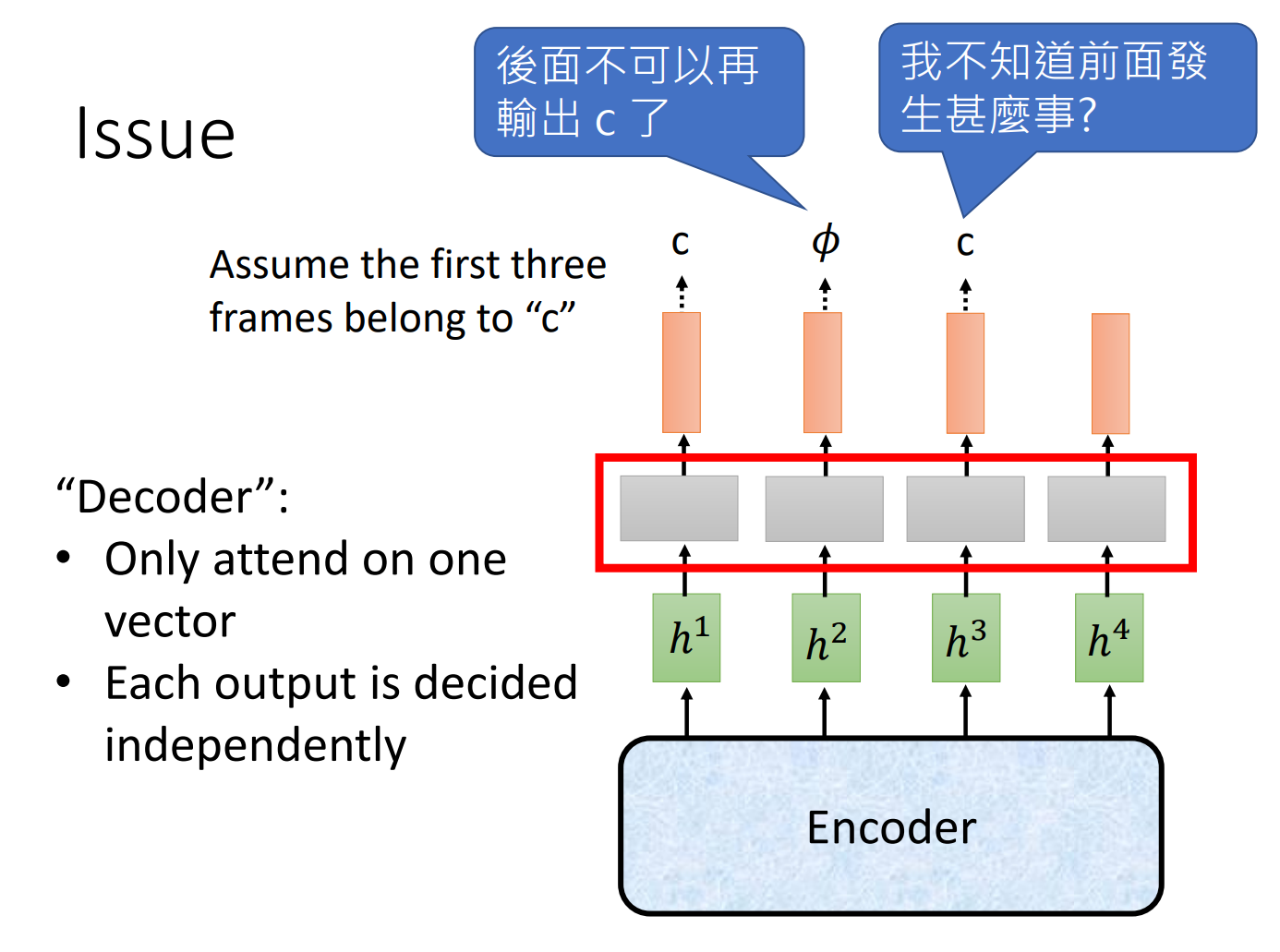
CTC 的训练中,可以通过引入简单的语言模型,例如 n-gram, 来提高ASR模型生成句子的合理性。但问题是其语言模型和声学模型是两个分离的独立结构。CTC的另一个缺点在于CTC存在累积效应, 即训练的模型对各个音素的可能性预测是尖峰似的,当每个音素的信息积累到一定程度才"蹦"出较高的概率。
RNN-T通过改进结构,使得系统可以同时显性地学习语言模型,使得声学模型和语言模型能够真正地统一学习,进一步促进系统性能。
2 RNN-T1
2.1 对齐方式
在讨论具体结构之前,首先先来了解Transducer 的对齐方式。Transducer 将状态切换以外的其他位置都标记为 $ \empty $ , 如 $y_1, y_2, y_3$ 和序列 $y_1, \empty , \empty , y_2 , \empty , y_3$ 等价。
2.2 结构
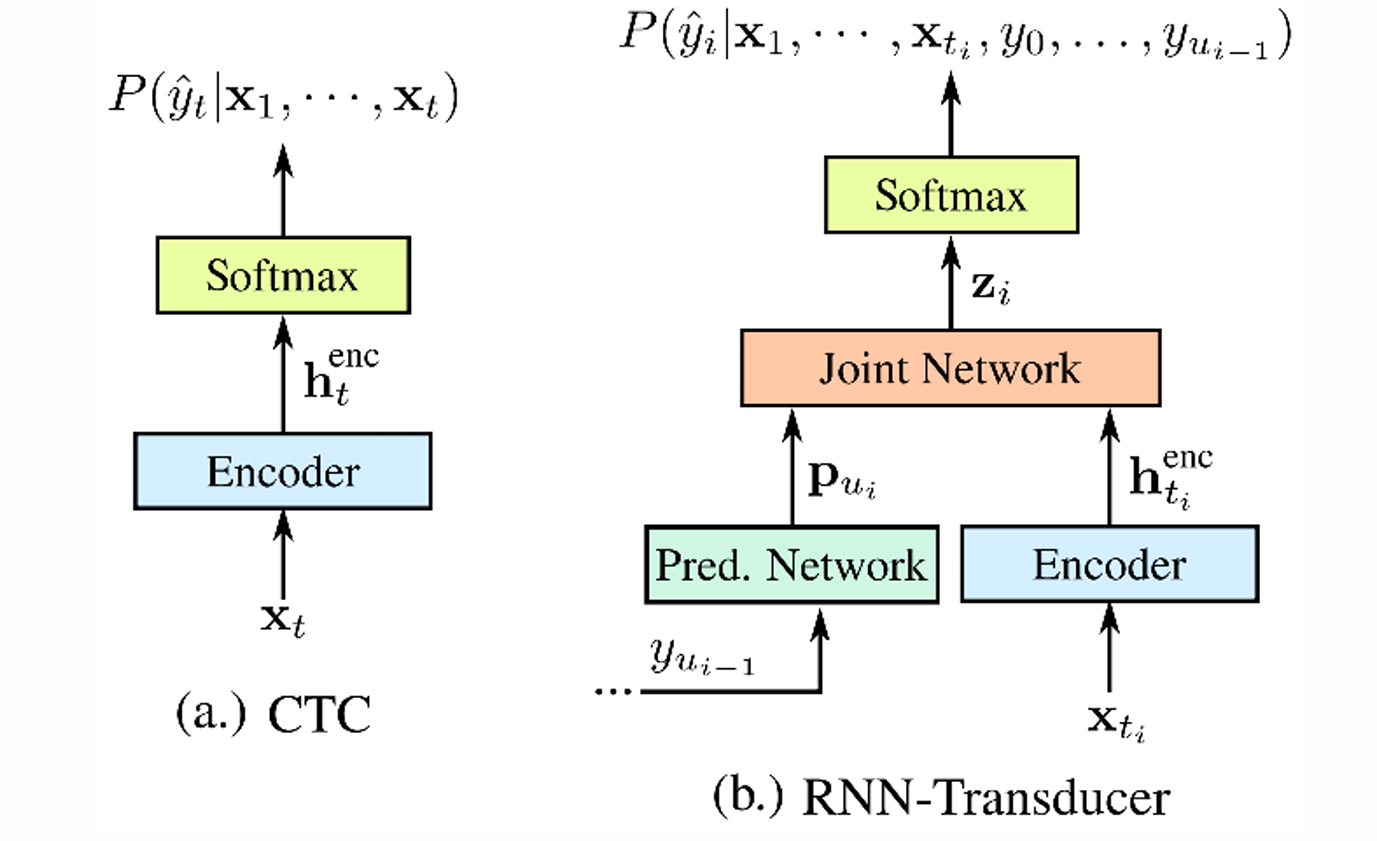
RNN-T 中最早提出了 Transducer 结构,如下图所示:
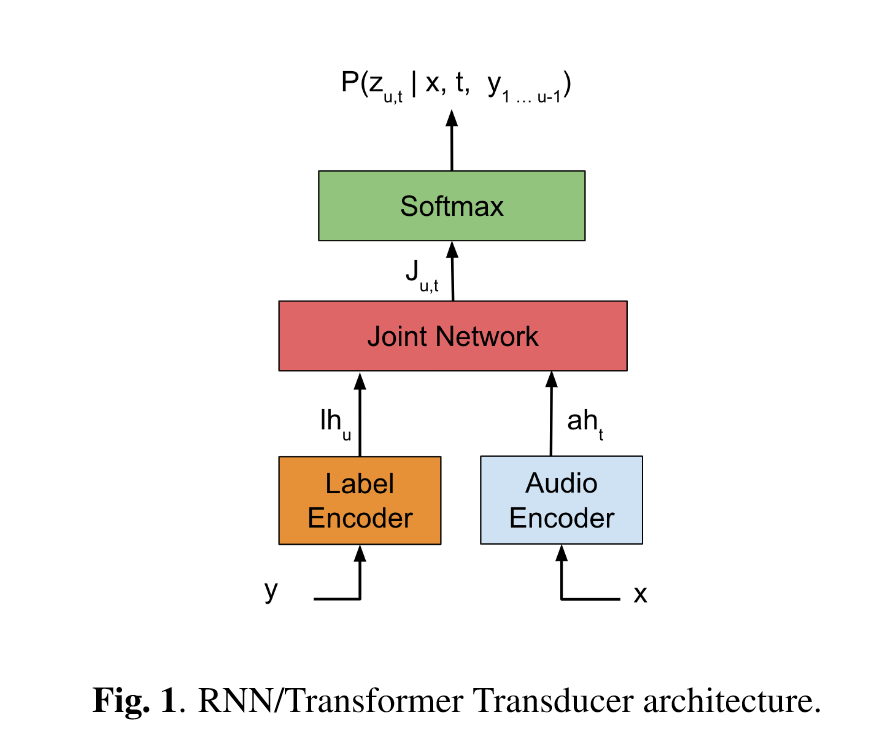
上图中,文本和音频分别通过编码器(在后来的部分文献中,也将文本编码器称作解码器)。在原始的RNN-T中,两者均为RNN结构(音频编码器两层LSTM,文本编码器一层LSTM)。之后通过一个 Joint 网络后,得到输出的概率矩阵。Joint 网络的结构如下图所示,其输出为输出概率矩阵。
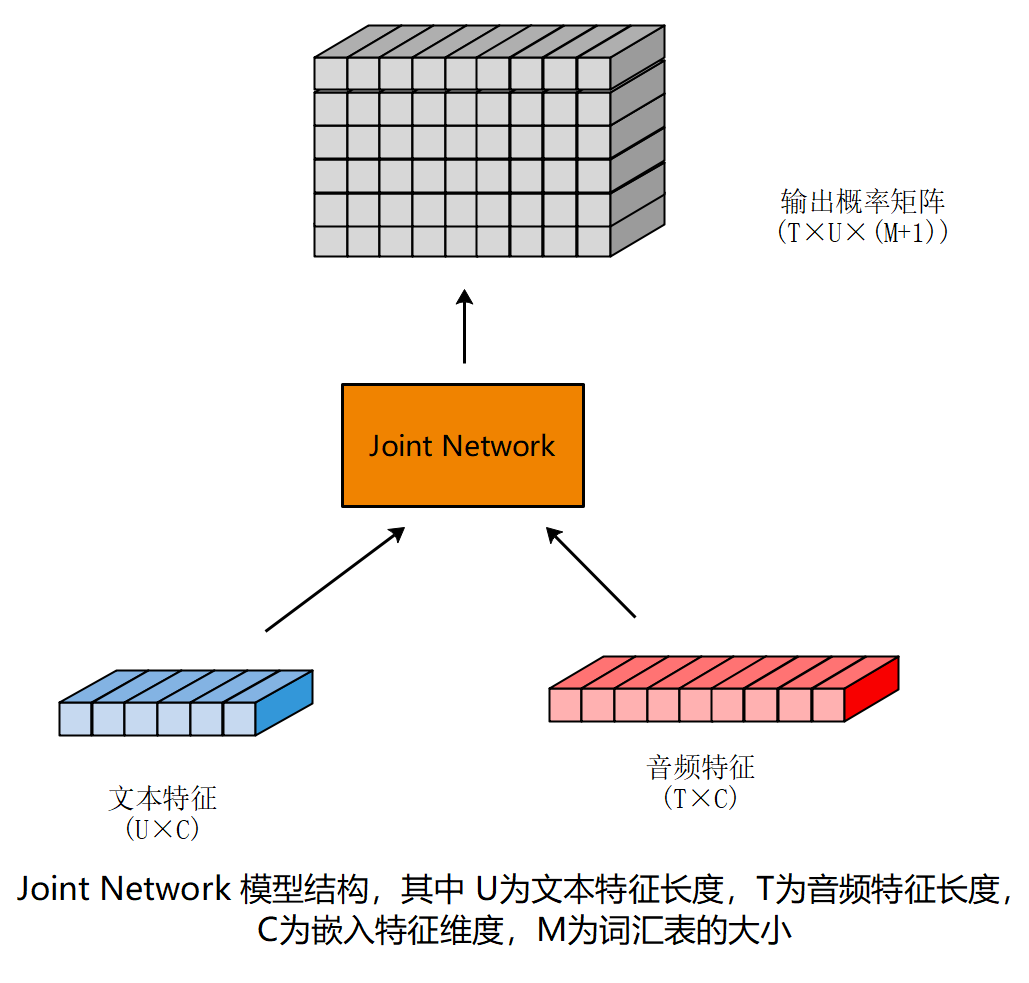
该矩阵的每一个坐标 $(t,u)$ 处的向量确定了该状态下的转移概率, 即如果在时刻 t, 对应的文本状态为 u, 那么下一跳转移到不同状态的概率。如果词汇表的大小一共为M,即有M种 文本 token, 那么考虑到 $ \empty $ 的存在,下一跳的状态数为 (M+1)。

对于上述的 $h(.)$ 函数, RNN-T 的定义方式为:
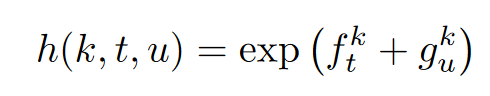
思考:为什么上式中 $f$ 和 $g$ 是相加而非相乘呢? 如何解释这里的相加?
2.3 训练与预测
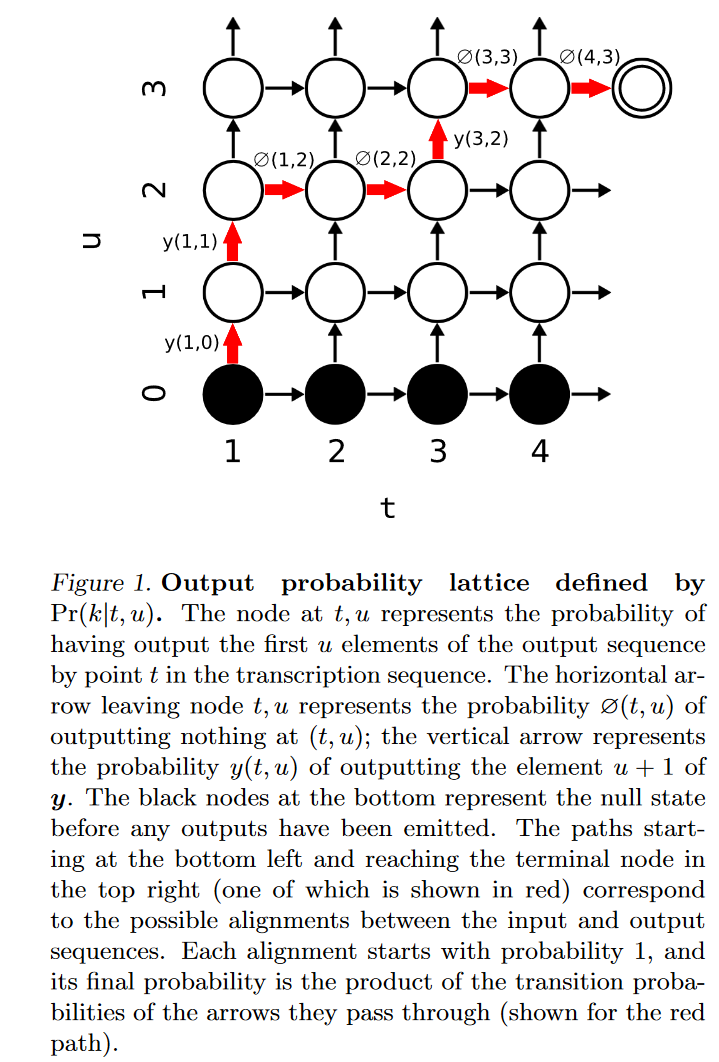
上述模型的输出为一个上图所示的概率矩阵。网格中存在若干条路径,每条路径代表一个可能的输出序列。在所有的这些序列中,合法的序列是起点为左下角,终点为右上角的序列。所有的合法序列之和即为输入为 $\bf{x}$ 的条件下输出 $\bf{y}$ 的概率。我们的优化目标是要最大化 $P(\bf{y} \vert \bf{x})$ 。

现在的问题是,该如何计算所有合法序列的和,要知道所有合法序列的数量为 $C^{U}_{T}$ 个,具有NP复杂度,肯定不能直接硬算。因而这里采用了动态规划的思想。
记从起点到达 $(t, u)$ 的概率为 $\alpha (t,u)$ , 从 $(t, u)$ 到终点的概率为 $\beta (t, u)$ 。那么从起点经由 $(t, u)$ 到达终点的概率自然为 $\alpha (t,u) \beta(t, u)$ 。我们可以通过动态规划的方式得到上述网格中每个点的 $\alpha$ 和 $\beta$ 。递推公式如下所示:
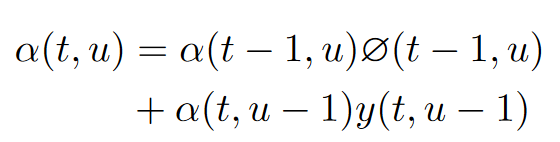
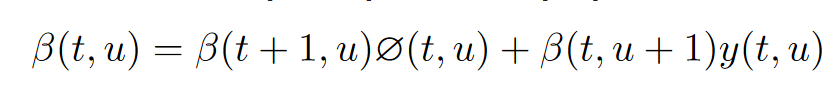
递推得到以上结果的时间复杂度仅为 $O(T\times U)$。下图展现了 网格中 $\alpha(t,u)$ , $\beta(t,u)$ 和 $\alpha(t,u) \beta(t,u)$ 的可视化。
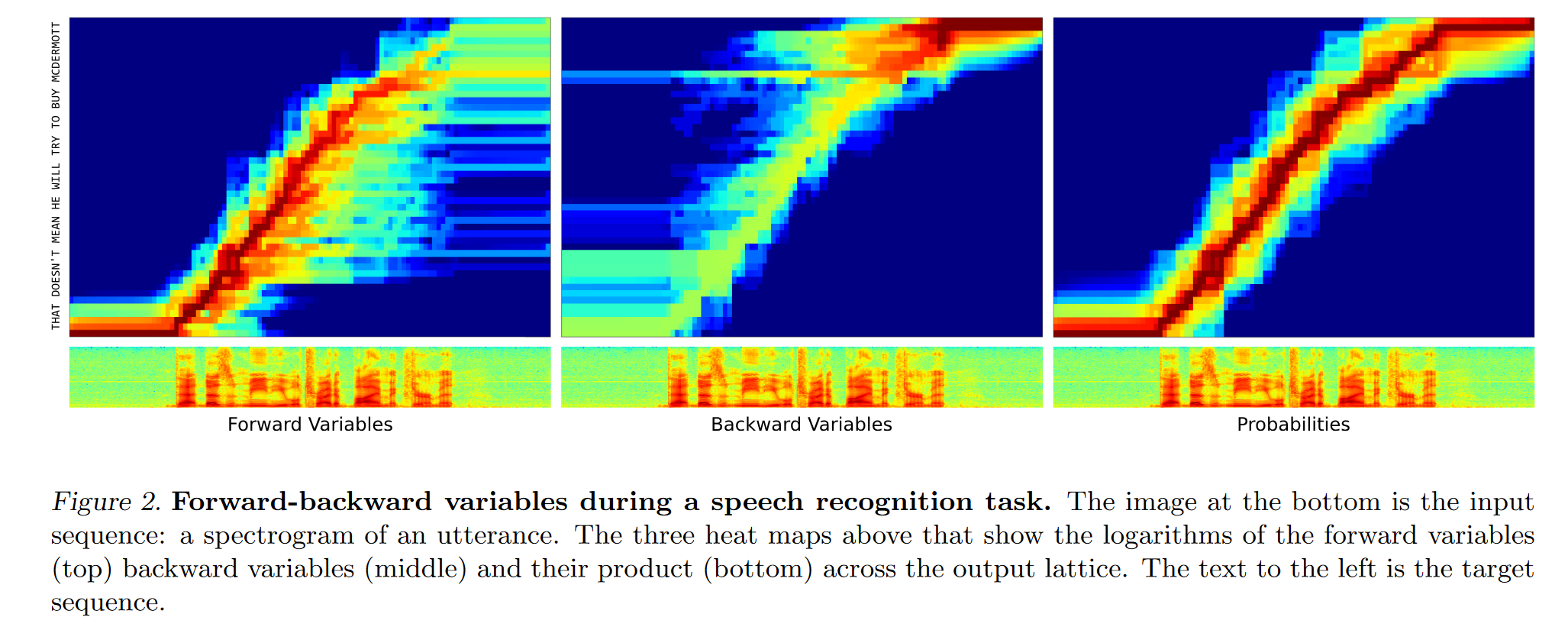
由于从起点到终点,一定会经过从图的左上角到右下角的斜对角线,我们可以据此分解概率如下:
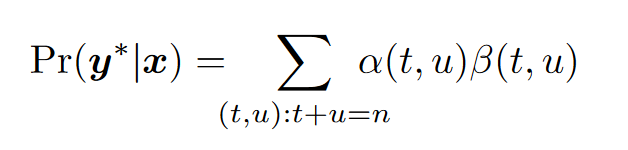
事实上这不是唯一的计算方式。也可以用 $\alpha(T,U)$ 的值作为优化目标(之后的transformer-Transducer 就是这么做的)。
在非流式的预测过程中,音频编码器输入完整的音频,得到音频嵌入特征。文本编码端(或者按照有些论文的说法,解码器端) 最开始输入<SOS> 标识(start of sentence)。解码的过程从音频特征的开始循环到结束,每次循环得到文本序列中下一个文本的概率。如果采用贪心法编码,则将每次预测结果中可能性最大的状态作为下一状态,如以下代码所示:
def greedy_search(model: Transducer, encoder_out: torch.Tensor) -> List[int]:
"""
Args:
model:
An instance of `Transducer`.
encoder_out:
A tensor of shape (N, T, C) from the encoder. Support only N==1 for now.
Returns:
Return the decoded result.
"""
assert encoder_out.ndim == 3
# support only batch_size == 1 for now
assert encoder_out.size(0) == 1, encoder_out.size(0)
blank_id = model.decoder.blank_id
device = model.device
sos = torch.tensor([blank_id], device=device, dtype=torch.int64).reshape(1, 1)
decoder_out, (h, c) = model.decoder(sos)
T = encoder_out.size(1)
t = 0
hyp = []
sym_per_frame = 0
sym_per_utt = 0
max_sym_per_utt = 1000
max_sym_per_frame = 3
while t < T and sym_per_utt < max_sym_per_utt:
# fmt: off
current_encoder_out = encoder_out[:, t:t+1, :]
# fmt: on
logits = model.joiner(current_encoder_out, decoder_out)
# logits is (1, 1, 1, vocab_size)
log_prob = logits.log_softmax(dim=-1)
# log_prob is (1, 1, 1, vocab_size)
# TODO: Use logits.argmax()
y = log_prob.argmax()
if y != blank_id:
hyp.append(y.item())
y = y.reshape(1, 1)
decoder_out, (h, c) = model.decoder(y, (h, c))
sym_per_utt += 1
sym_per_frame += 1
if y == blank_id or sym_per_frame > max_sym_per_frame:
sym_per_frame = 0
t += 1
return hyp
而如果采用 beam-search, 则每次搜索时需要保留概率最大的两个路径,详细做法见原论文伪代码。
注意同一帧可能解码出多个 token 的情况,如 $ABC \empty D$ 的 ABC 是连着的。
3 Transformer-T2
本文主要贡献为:
- 利用Transformer结构 (Transformer-XL) 代替了RNN-T 中的LSTM;
- 说明基于 Transformer-XL 的Transformer-T适合进行流式的语音识别;
3.1 对 Joint 层的改进

3.2 Transformer-XL3
该模型使用的 Transformer 结构为 transformer-XL。该结构相对于原始 transformer的改进为以下两点
3.2.1 Segment-Level Recurrence with State Reuse
原始的 Transformer 对于过长的序列面临计算量等问题。一种基本的思路是分块解决。但这种思路的问题是,对块边缘的点,会由于缺失上下文导致效果不佳。 Transformer-XL 对此的改进方案是采用了递归的策略,将上一个块的特征 $h_\tau$ 和 本层的特征 $h_{\tau+1}$ 直接进行拼接,区别在于之前块的特征不进行反向传播。

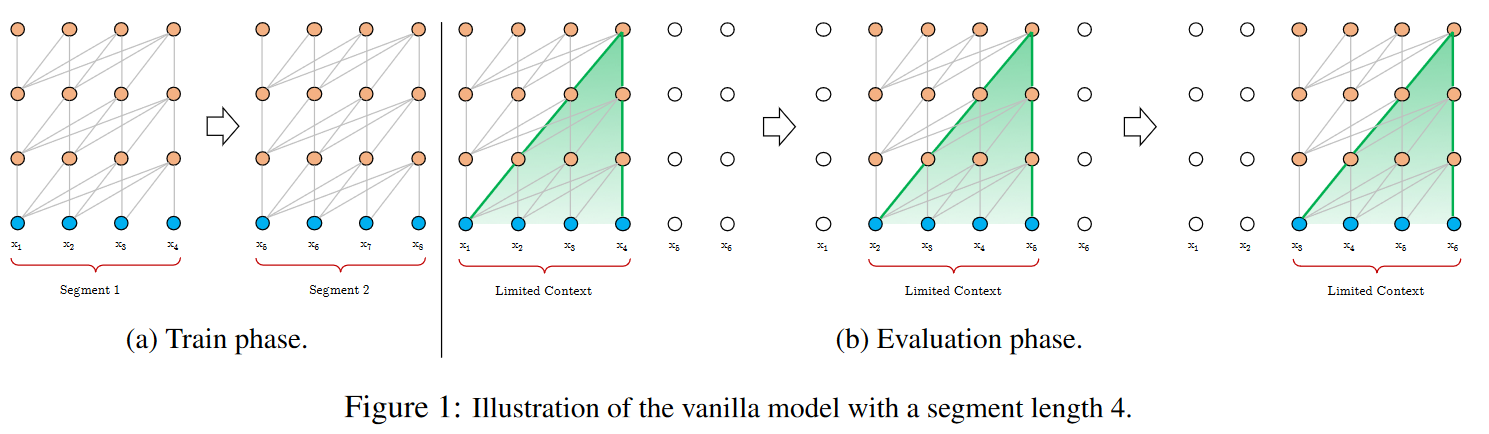
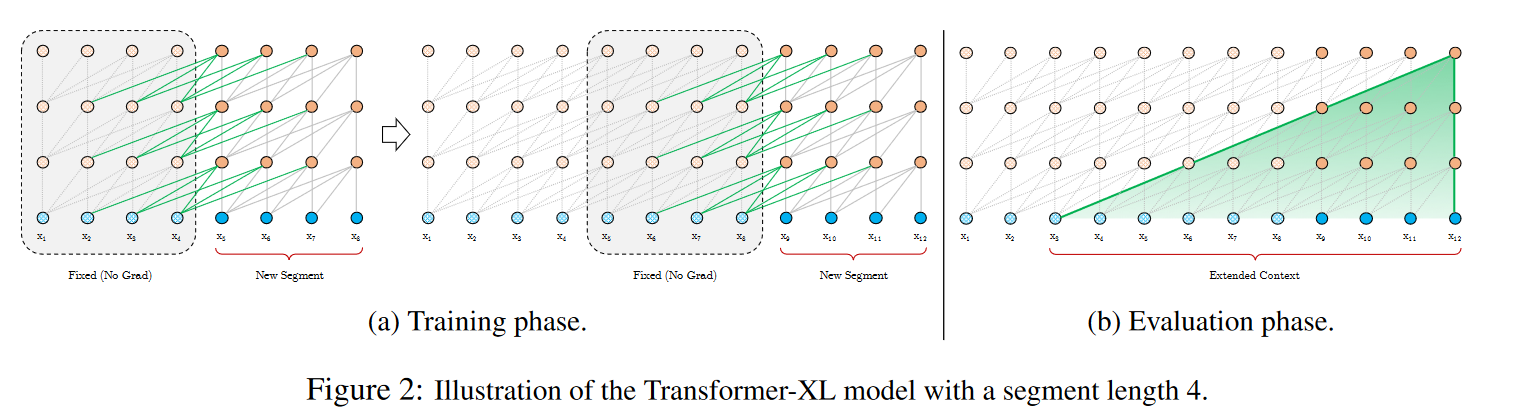
这样做不仅能够建立起快与块之间的上下文关联,同时预测时可以将之前块attention的计算结果缓存起来,以供之后使用。因此该结构相当适合用于流式语音处理。
注:NLP中编码器和解码器的区别:
一般NLP中谈到编码器和解码器,均指 "Transformer is All you need" 里面的编码器和解码器结构。两者最大的区别在于,编码器可以看到整个序列,但解码器只能看到过去。因而我们可以说,上文的 transformer-XL 就是一个纯解码器的结构。编码器模型和解码器模型的典型代表是bert 和 GPT。
3.2.2 相对位置编码
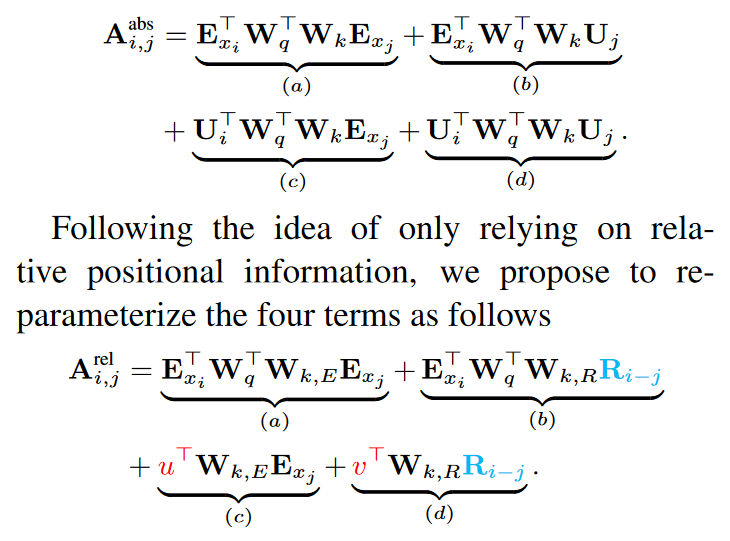
3.3 实验设置与结果
- 该模型处理将频谱图转化成token的方法是将4帧拼接成一帧作为token( Frame-based);
- 模型结构为
- 音频编码器:18层 transformer block;
- 文本编码器: 2层 transformer block;
- 实验结果表明该模型可以在 LibriSpeech 语料库上取得SOTA性能;
- 作者讨论了流式模型中上下文(context)大小对性能的影响;
4 Conformer-T4
作者认为,transformer 虽然善于建模长时依赖性,但不善于提取细粒度的局部特征。而CNN则比较擅长捕捉局部信息(由于其局部性)。之前的工作5将CNN和transformer串联结合,如下图所示。
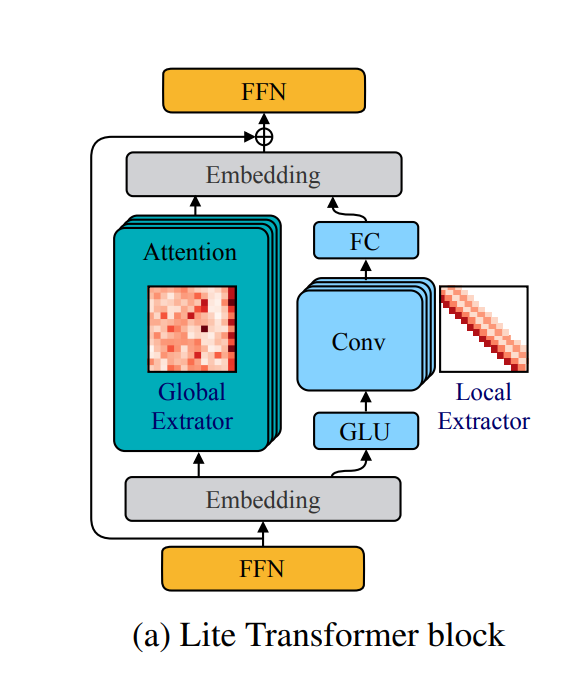
本文延续这一思路,研究如何将卷积和自注意力有机结合起来。为了实现这一目标,作者提出了一种自注意力和卷积的新颖组合,希望实现两全其美的方案——自注意力学习全局交互,而卷积有效捕获基于相对偏移的局部相关性。
模型结构如下所示,其创新点为:
-
"马卡龙状"的前馈层, 每个前馈网络只有1/2的权重;
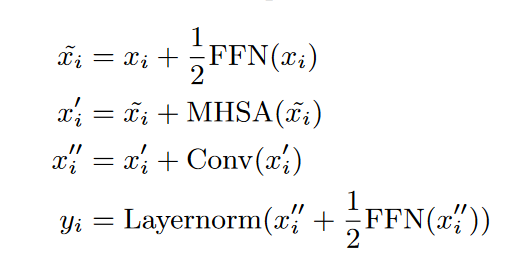
- CNN 的设计思路同 mobile-Net, 采用深度可分离卷积(逐层-逐点), 以节省计算量;
- attention 仍然使用了transformer-XL中的相对位置编码;
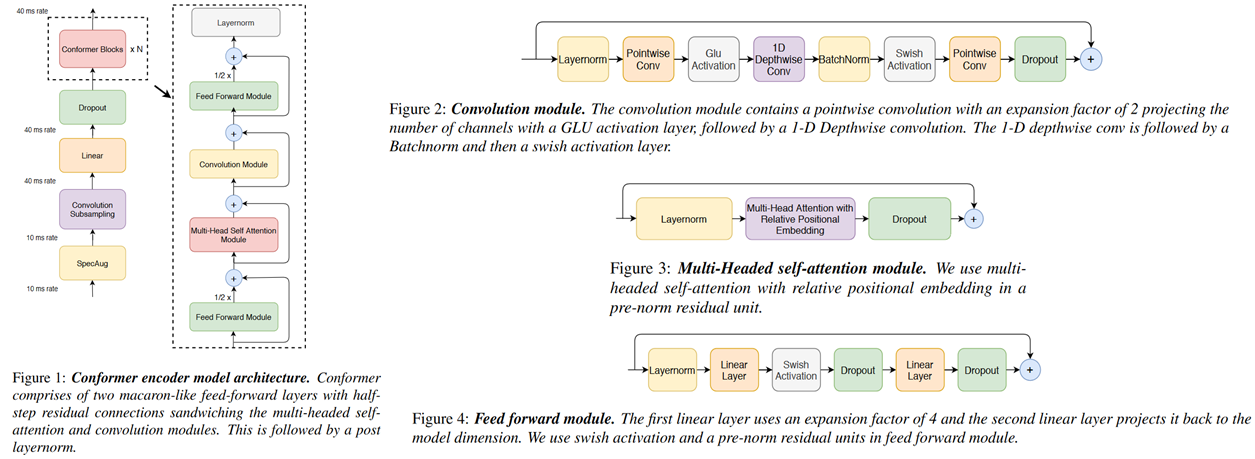
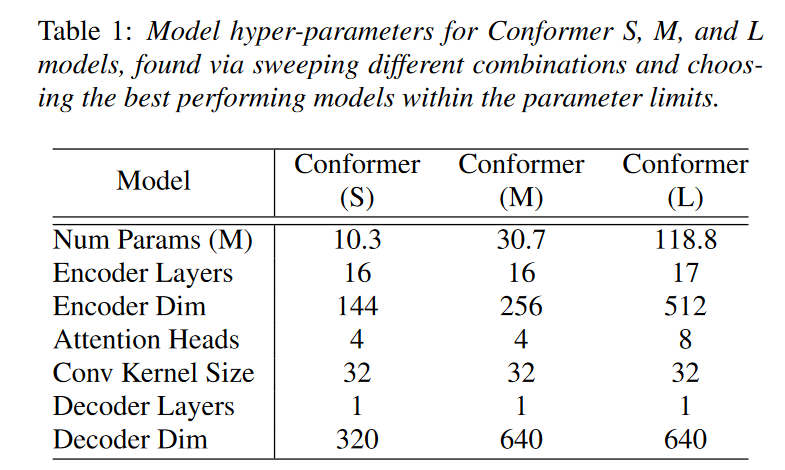
模型具体结构:
此外,在纯文本语料库上训练了3层LSTM用于语言模型。
Reference
-
Sequence Transduction with Recurrent Neural Networks, 2012 ↩
-
TRANSFORMER TRANSDUCER: A STREAMABLE SPEECH RECOGNITION MODEL WITH TRANSFORMER ENCODERS AND RNN-T LOSS, ICASSP2020 ↩
-
Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context ↩
-
Conformer: Convolution-augmented Transformer for Speech Recognition, interspeech2020 ↩
-
LITE TRANSFORMER WITHLONG-SHORT RANGE ATTENTION , ICLR2020 ↩