Flow
1 Normalizing Flows
在笔记 ‘生成式算法概述' 中，我们已经对 Normalizing Flows 技术有了大致的了解，其通过以下公式将输入的高斯分布转化为目标分布:
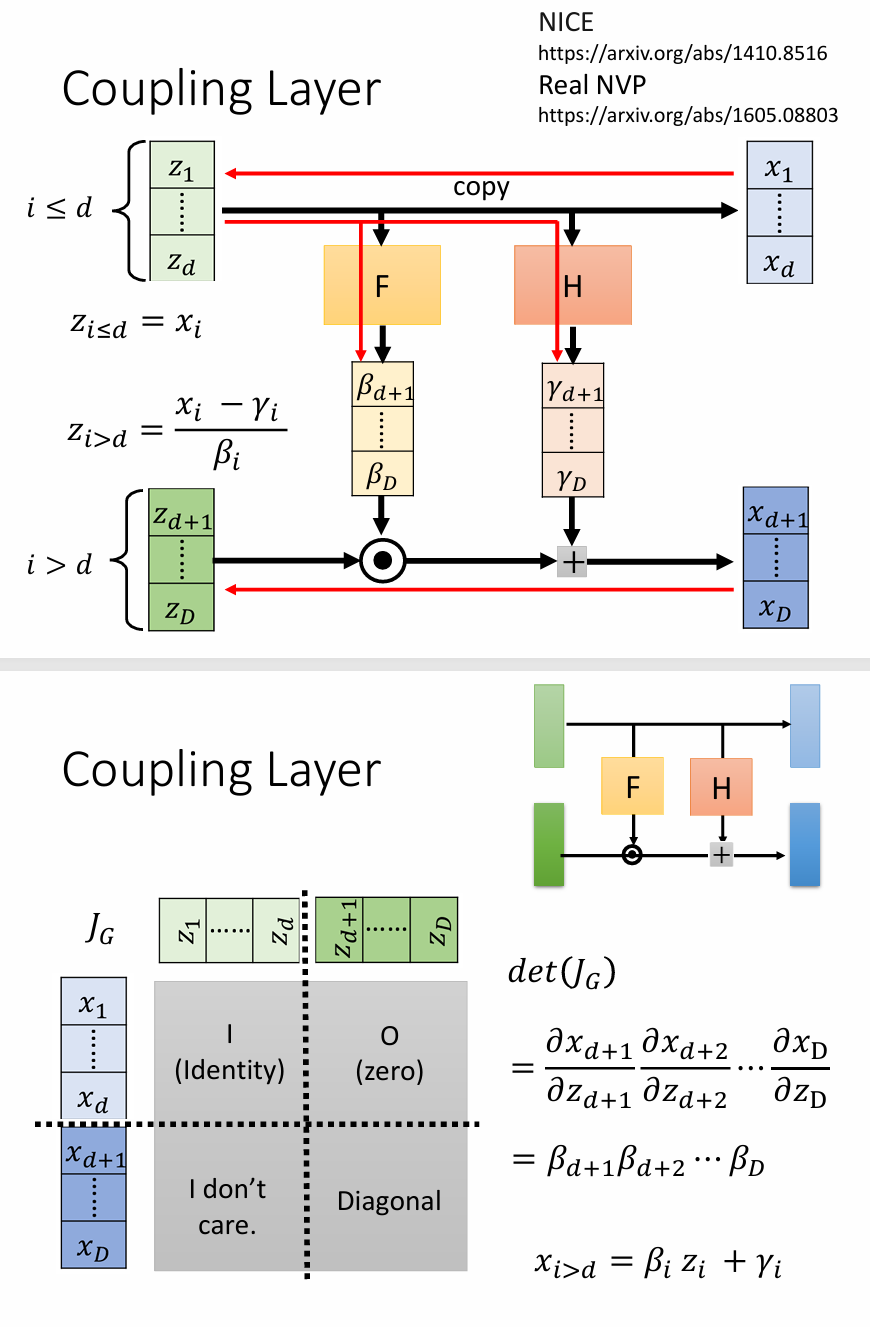
\[p_{G}(x)=\left| J_{G^{-1}} \right|\pi(G^{-1}(x))\]关于如何设计网络，使得雅可比矩阵的行列式可知, 目前应用较多的策略是基于Coupling Layer的策略，其结构如下图所示:
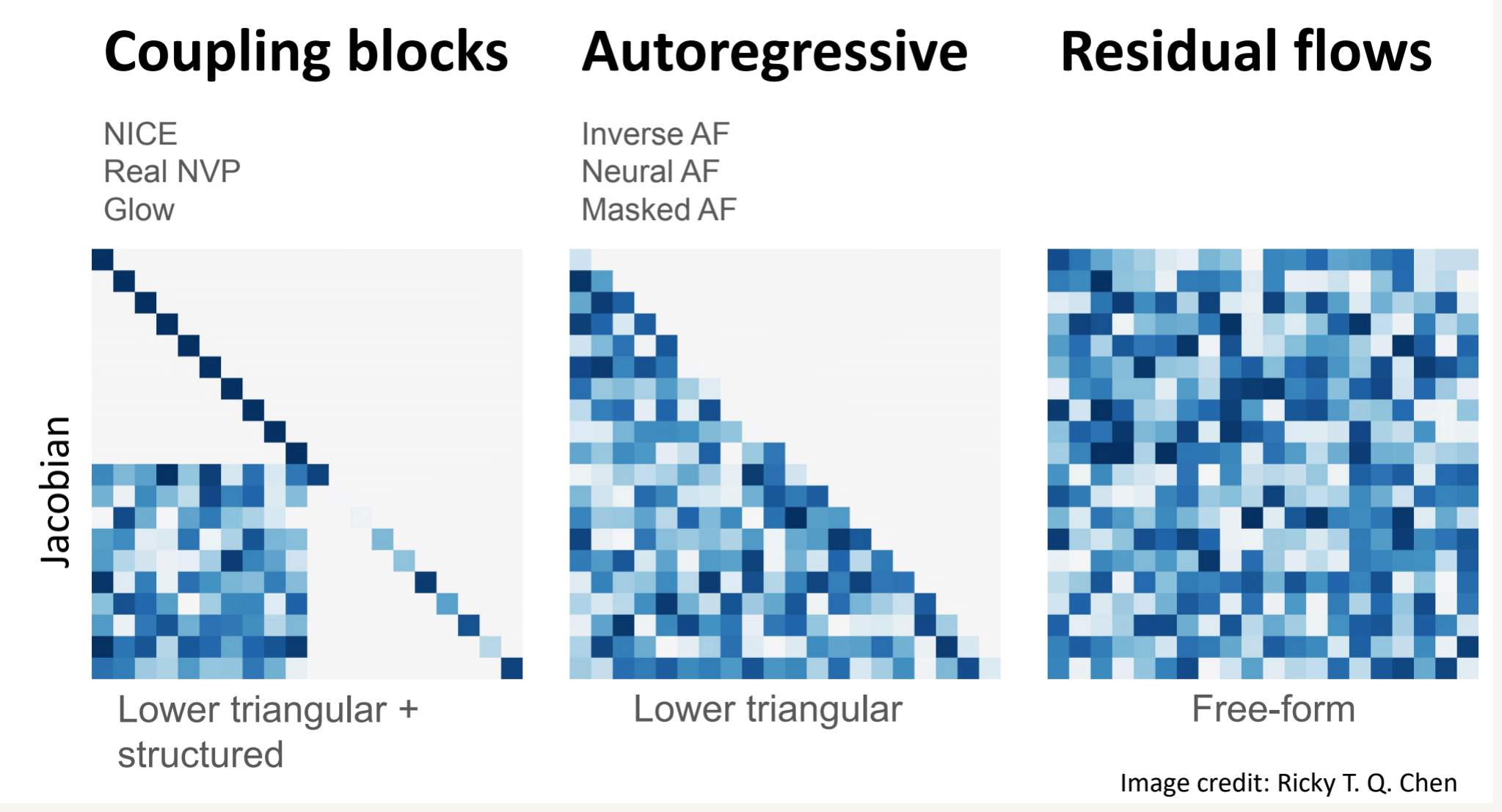
下图展现了几种常见的 Normalizing Flows 的实现策略，可以看到 Coupling Layer 策略的雅可比矩阵容易计算，但缺点是由于对其形式的限制，导致其函数的表现力不足。而对于下图的 Residual flow, 其具有形式 $x = z+u(z)$ , 即每一次更新残差。该方法虽然限制少，表现力强，但缺点在于雅可比矩阵不容易计算。
2 Continuous Normalizing Flows
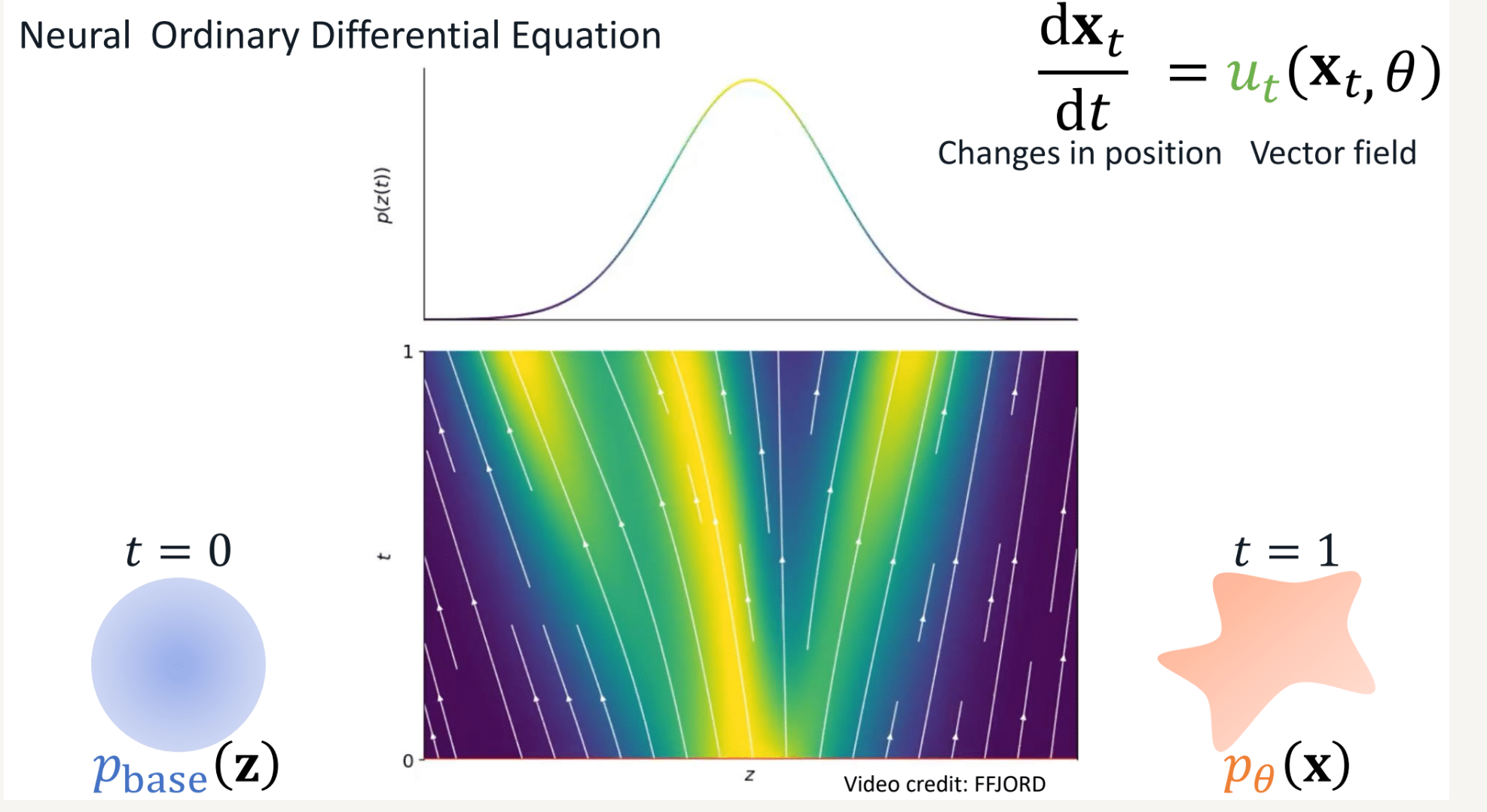
注意到在 residual flows 中，可以通过每次更新残差的方式，让分布逐渐从高斯分布变到目标分布。假设这一更新过程是连续的，而不是离散的，那么可以用以下形式表示更新:
\[\frac{dx_t}{dt}=u_t(x_t, \theta)\]在 Continuous Normalizing Flows 中，将 $u_t$ 称为向量场(Vector field)， 该方法将从数据从高斯分布演变到目标分布，视作为通过场来实现的，如下图所示
这里将概率类比为流体，由于总的概率积分是1，就类似于流体的总量是一定的，因此对x点来说，有以下公式(Continuity Equation)成立
\[\frac{\partial p_t(x)}{\partial t} + \text{div} \left( p_t(x) u_t(x) \right) = 0\]该公式的含义是某处概率密度的变化等于"流出"和"流入"x概率的"流量"之差。该公式是是向量场 u 产生对应的概率密度路径 p(x)的充要条件。换句话说，已知 $p_t$ 的情况下，只要找到一个符合上述等式的 $u_t$ , 那么该$u_t$ 就一定是合理的。
3 Flow Matching
Continuous Normalizing Flows 并不好求解，因为想要找到合适的 u 并不容易。Flow Matching 的思想是，构建一个模型，来学习去预测这个场。
\[L_{\text{FM}} = \mathbb{E}_{t, p_t(\mathbf{x}_t)} \left[ \left\| v_t(\mathbf{x}_t, \theta) - u_t(\mathbf{x}_t) \right\|_2^2 \right]\]可以将总的概率视作通过对条件概率进行边缘积分得到：
\[p_t(\mathbf{x}_t) = \int p_t(\mathbf{x}_t | \mathbf{z}) \, q(\mathbf{z}) \, d\mathbf{z}\]而也可以证明在数据点 x 处的向量场 $u_t(x)$ 是通过对所有可能的初始条件 x1 的条件向量场$ u_t(x∣x_1)$ 加权积分得到。 这里的z作为条件，其设置是灵活的。根据条件z的不同，flow matching 可以分为三种不同情况:
3.1 conditional flow matching
首先假设已知生成目标, 即路径的终点是x1。只要满足如下两个边界条件，就能作为条件概率路径 $p_t$ ：
- t=0时是标准高斯分布;
- t=1时服从以均值为x1, 方差足够小的高斯分布;
而当构造了路径 $p_t$ 之后，变化速度 $u_t$ 也可以根据 Continuity Equation 构造出来。总而言之，对CFM 我们有以下的路径p和速度u
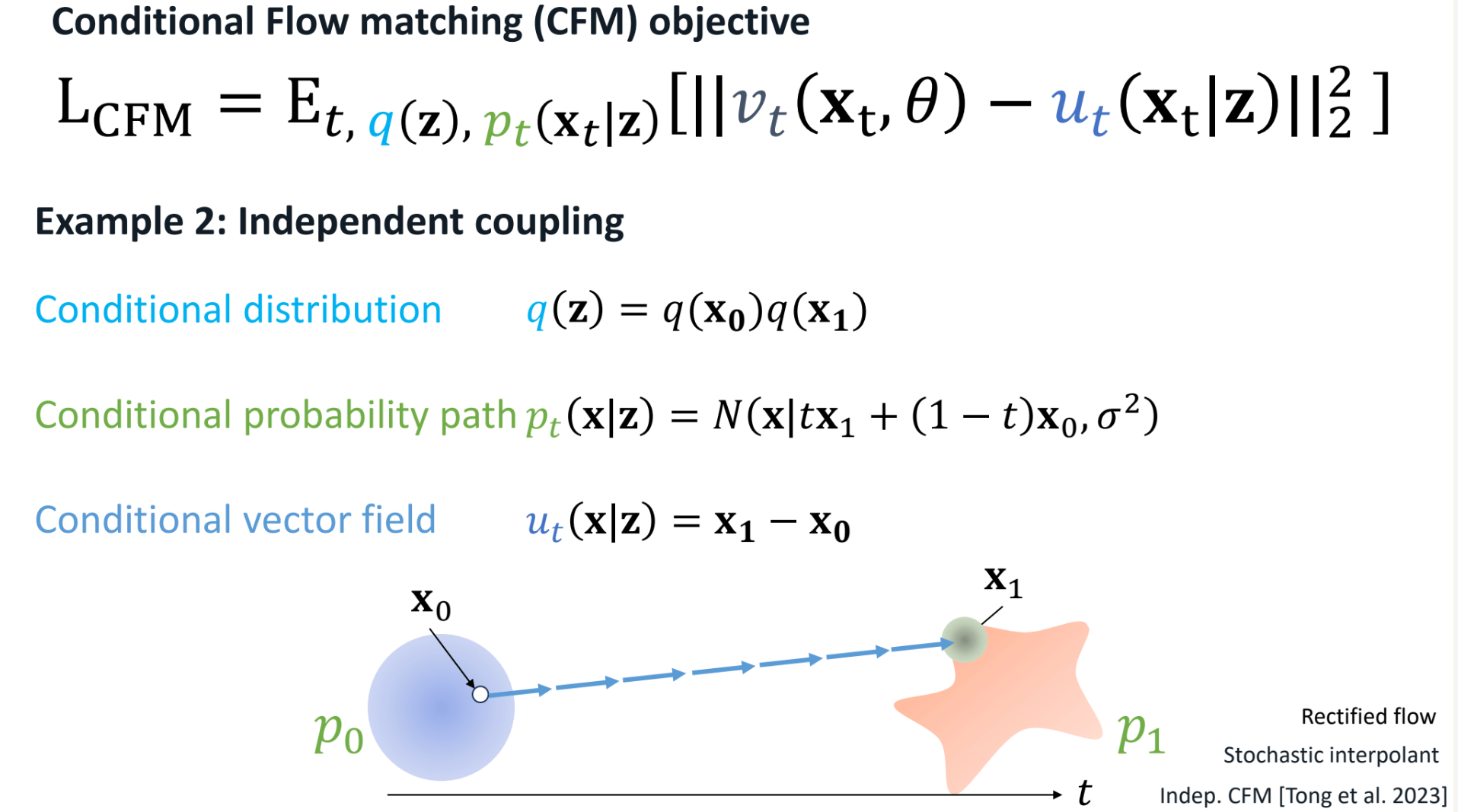
3.2 Independent coupling (I-CFM)
该条件下假设 x1 和 x0 均已知且独立，这种情况下路径如下。
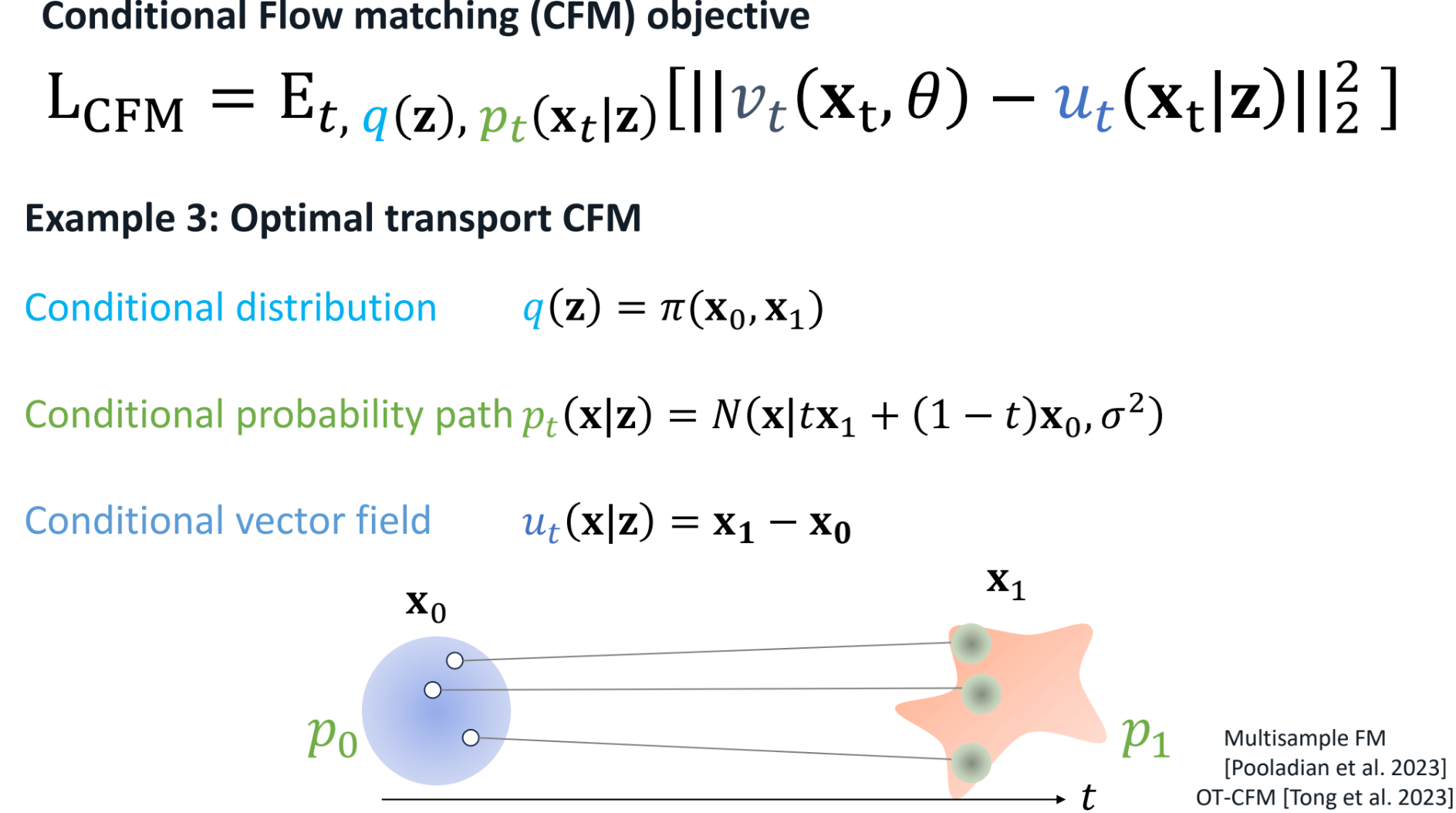
3.3 Optimal transport CFM (OT-CFM)
在有多个x0和x1的情况下，OTT-CFM根据最佳传输理论, 为x0分配最优的x1，如下图所示
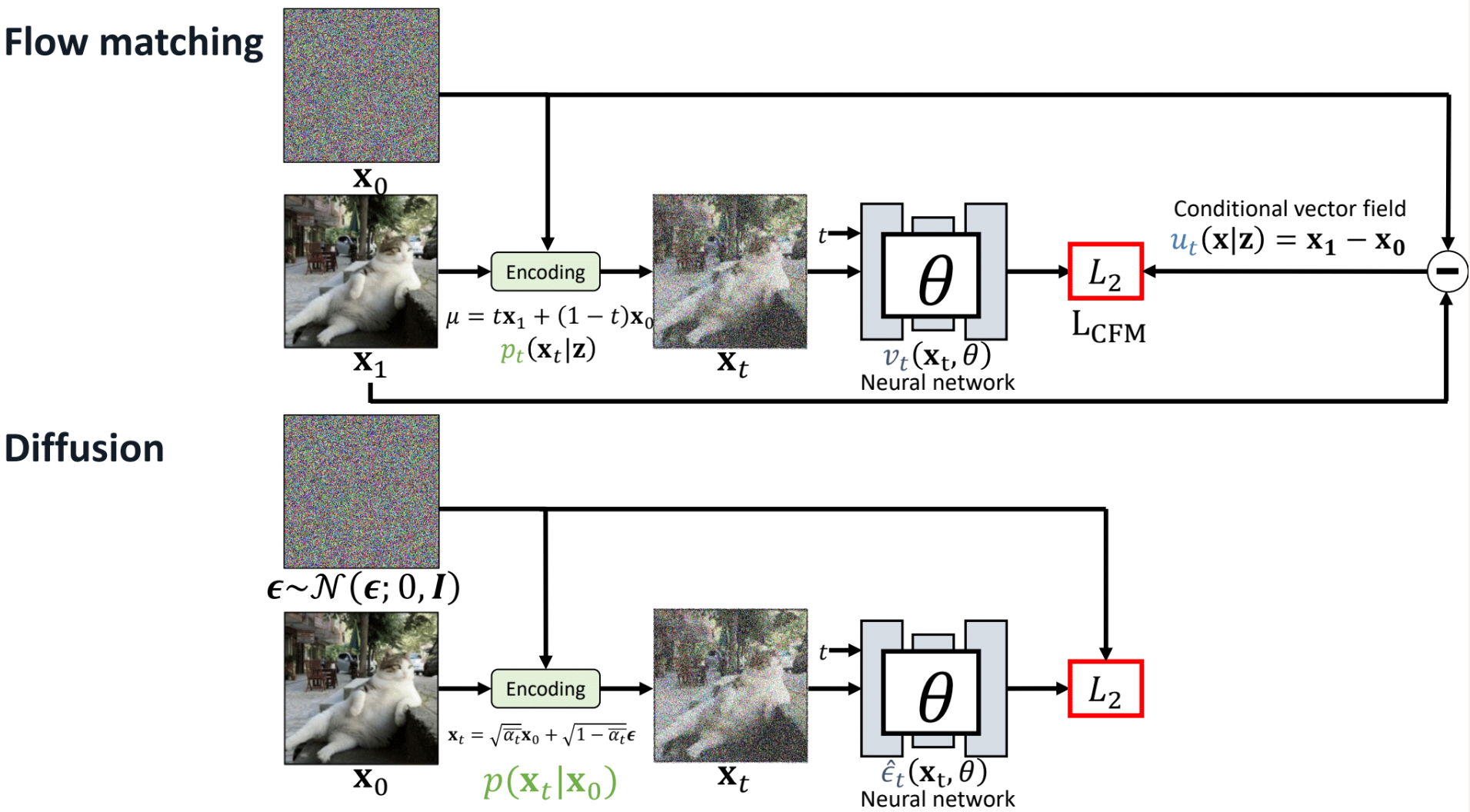
3.4 与 Diffusion
Flow match允许使用各种可微分函数来定义p和u ，所以可以根据不同的应用场景和边界条件选择合适的函数。例如，可以将 flow matching 与diffusion 结合1。实验发现，将扩散模型条件向量场与Flow Matching目标结合起来优化，相比于现有的Score Matching方法，训练收敛更快更稳定2。
3.5 如何训练
Flow matching 的训练过程如下。可以看到，该方法和diffusion的训练过程高度相似。所以说虽然二者来源可能不一样，但最后实践下来形式是高度相似的。
